Tan^2x identity 120176-Tan 2x identity

Derivation of Tan2x Formula Tan2x Formula = tan x 2 tan x 1 − t a n 2 x Now, we need to recall the addition formula, tan a tan b tan a tan b t a n ( a b) = tan a tan b 1 − tan a tan b So, for the double angle formula, here let the values of both the angles be a (a = b) tan a tan a tan a tan a t a n ( a a) = tan a tan a 1A trigonometric identity that expresses the expansion of cosine of double angle in cosine and sine of angle is called the cosine of double angle identity Introduction When the angle of a right triangle is denoted by a symbol theta, the cosine and sine of angle are written as $\cos{\theta}$ and $\sin{\theta}$ respectively In the same way, theIdentidades de ângulo múltiplo gratuitas passo a passo para listar as identidades de ângulo múltiplo por solicitação

Topic Lesson Trigonometric Functions

Tan 2x identity

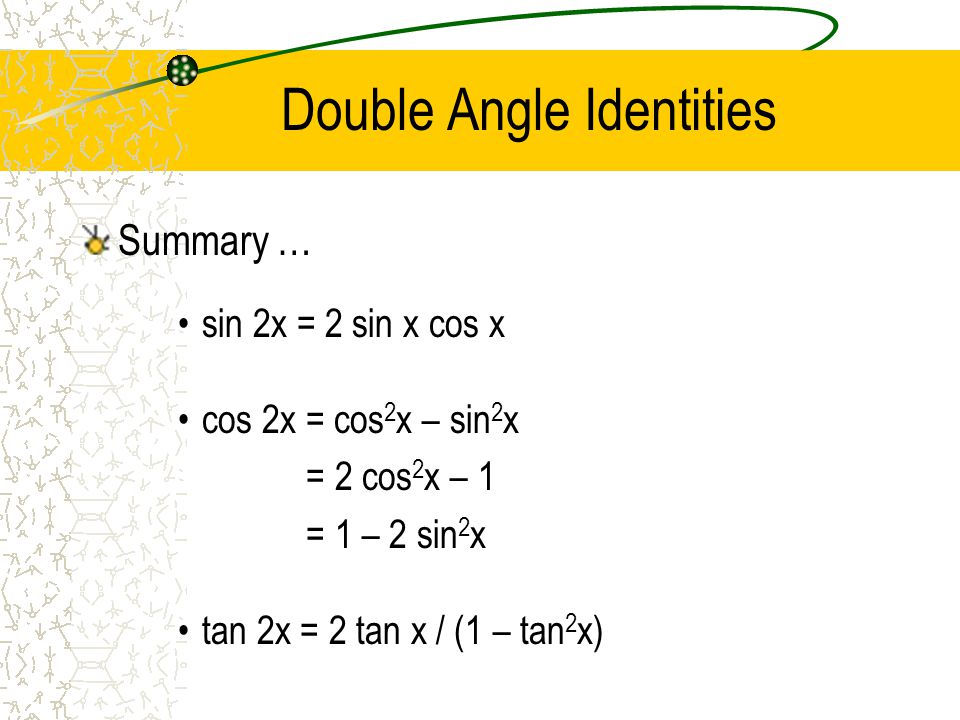
Tan 2x identity-Sin (x y) = sin x cos y cos x sin y cos (x y) = cos x cosy sin x sin y tan (x y) = (tan x tan y) / (1 tan x tan y) sin (2x) = 2 sin x cos x cos (2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan (2x) = 2 tan (x) / (1 tan ^2 (x)) sin ^2 (x) = 1/2 1/2 cos (2x) cos ^2 (x) = 1/2 1/2 cos (2x) sin x sin y = 2 sin ( (x y)/2 ) cos ( (x y)/2 )Identity\\tan(2x) doubleangleidentitiescalculator identidade \tan(2x) ar Related Symbolab blog posts High School Math Solutions – Trigonometry Calculator, Trig Identities In a previous post, we talked about trig simplification Trig identities are very similar to this concept An identity

Every Day I M Calculatin I D3 Unit Q Pythagorean Identities

 asked Prove the identity 1 2 csc ⁡ 2 x = cos 2 x tan ⁡ x Choose the sequence of steps below that verifies the identity A) cos 2 x tan= 1 – 2 sin2 x = 2 cos2 x – 1 • Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;Question I need to prove the identity (1tan^2x)cot^2x=csc^2x Found 2 solutions by Alan3354, Regrnoth Answer by Alan3354() (Show Source) You can put this solution on YOUR website!

Tan 2x ≠ 2 tan x by Shavana GonzalezVerify the identitytan 2 x (1 cos 2x) = 1 cos 2x asked in Mathematics by tommys algebraandtrigonometry;Transcribed image text Verity the identity tan^2x sin^2 cos^2x = secºx To verify the identity, start with the more complicated side and transform it to look like the other side Choose the correct transformations and transform the expression at each step tan?zx sin 2x cos2x Factor out the greatest common factor Apply a Pythagorean identity to the sum of the second and third term

Basic Trig Identities The basic trig identities or fundamental trigonometric identities are actually those trigonometric functions which are true each time for variablesSo, these trig identities portray certain functions of at least one angle (it could be more angles) It is identified with a unit circle where the connection between the lines and angles in a Cartesian planeLegend x and y are independent variables, ; How to prove the trigonometry equation is an identity?

Double Angle Identities Solutions Examples Videos Worksheets Games Activities

Every Day I M Calculatin I D3 Unit Q Pythagorean Identities

T a n 2 x = s i n 2 x c o s 2 x We substitute these back to our equation to get t a n 2 x 1 = s e c 2 x We immediately notice that there is a 1 t a n 2 x in the denominator of the expression we want to solve for, so we can use this identity to get t a n 2 x 1 t a n 2 x = t a n 2 x s e c 2 xD is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4Verify that each equation is an identitycos4 x =

Section 2 Identities Cofunction Double Angle Half Angle Ppt Video Online Download

2

Tan(2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin(2x) to cos(2x) sin(2 x) = 2 sin(x) cos(x) cos(2 x) = (cos(x))^2 – (sin(x))^2 =Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor Here we will prove the problems on trigonometric identities As you know that the identity consists of two sides in equation, named Left Hand Side (abbreviated as LHS) and Right Hand Side (abbreviated as RHS)To prove the identity, sometimes we need to apply more fundamental identities, eg $\sin^2 x \cos^2 x = 1$ and use logical steps in order to lead one

Double Angle Identities

Topic Lesson Trigonometric Functions

Section 52 Solutions 1 The cofunction identities apply to complementary angles Viewing the two acute angles of a right triangle, if one of those angles measures x x, the second angle measures π 2 −x π 2 − x Then sinx =cos(π 2 −x) sin ( π 2 − x) Derive Double Angle Formulae for Tan 2 Theta T an2x= 2tanx 1−tan2x T a n 2 x = 2 t a n x 1 − t a n 2 x let's recall the addition formula tan(ab) = tanatanb 1−tanatanb t a n ( a b) = t a n a t a n b 1 − t a n a t a n b So, for this let a = b , it becomes tan(aa) = tanatana 1−tanatana t a n ( a a) = t a n a t a n a 1 − t a n a t a n aCos 2x ≠ 2 cos x;

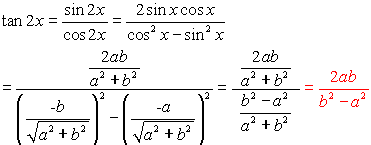
Six Trigonometric Functions Mathbitsnotebook Ccss Math

Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube

 Yes, sec 2 x−1=tan 2 x is an identity sec 2 −1=tan 2 x Let us derive the equation We know the identity sin 2 (x)cos 2 (x)=1 ——(i) Dividing throughout the equation by cos 2 (x) We get sin 2 (x)/cos 2 (x) cos 2 (x)/cos 2 (x) = 1/cos 2 (x) We know that sin 2 (x)/cos 2 (x)= tan 2 (x), and cos 2 (x)/cos 2 (x) = 1 So the equation (i) after substituting becomes Get an answer for 'Prove tan^2x sin^2x = tan^2x sin^2x' and find homework help for other Math questions at eNotes How to prove the identity `sin^2x cos^2x = 1` ?

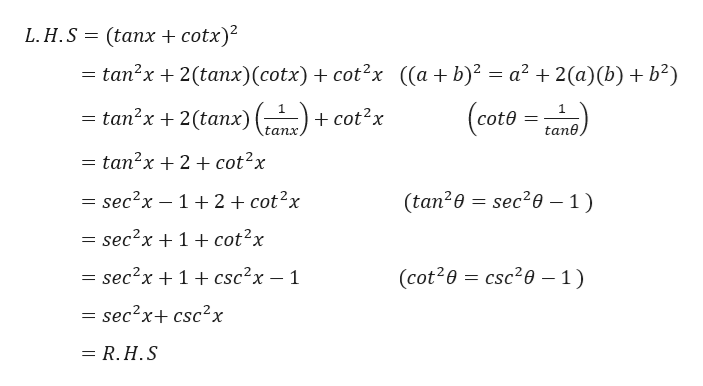
Answered The Question Says To Confirm That The Bartleby

Solved Verify The Identity 4 2 Tan X Secx2tan X 1 Which Chegg Com

Question Prove each identity tan^2x sin^2x = tan^2xsin^2x Answer by greenestamps(9506) (Show Source) You can put this solution on YOUR website!You have seen quite a few trigonometric identities in the past few pages It is convenient to have a summary of them for reference These identities mostly refer to one angle denoted θ, but there are some that involve two angles, and for those, the two angles are denoted α and β The more important identities When trying to prove trig identities, it is often helpful to convert TAN functions into SIN/COS functions Proof Step 1 Start with the original equation to prove tan2x sin2x = (tan2x)(sin2x) Proof Step 2 Replace tan with sin/cos (sin2x/cos2x) sin2x = (sin2x/cos2x)(sin2x)

Solved Review The Following Derivation Of The Tangent Double Angle Identity The Steps Are Not Listed In The Correct Order Course Hero

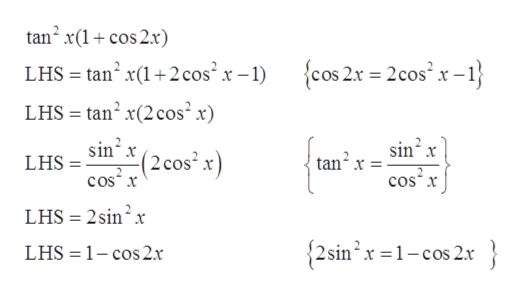
Answered Tan2x 1 Cos2x 1 Cos2x Verify The Bartleby

 Proving trig identity $\tan(2x)−\tan(x)=\frac{\tan(x)}{\cos(2x)}$ Ask Question Asked 4 years, 2 months ago Active 4 years, 2 months ago Viewed 4k times 1 1 $\begingroup$ I'm currently stumped on proving the trig identity below $\tan(2x)\tan (x)=\frac{\tan (x)}{\cos(2x)}$ Or, alternatively written asTrigonometry Q&A Library Verify the identity tan2x csc2x – cot2x= sec²2x To verify the identity, start with the more complicated side and transform it to look like the other side Choose the correct transformations and transform the expression at each step tan 2x csc 2x cot 2x 2х 2, 2 = sec 22x Apply a Pythagorean identity to the difference of the second and third termProve tan^2 (x)sin^2 (x)=tan^2 (x)sin^2 (x) Trigonometric Identities Solver Symbolab Identities Pythagorean Angle Sum/Difference Double Angle Multiple Angle Negative Angle Sum to Product Product to Sum

Tan2x ただの悪魔の画像

Fastest Is Tan 2x Cot 2x 1 An Identity

To integrate tan^22x, also written as ∫tan 2 2x dx, tan squared 2x, (tan2x)^2, and tan^2 (2x), we start by utilising standard trig identities to change the form of the integral Our goal is to have sec 2 2x in the new form because there is a standard integrationThese identities are useful whenever expressions involving trigonometric functions need to be simplified An important application is the integration of nontrigonometric functions a common technique involves first using the substitution rule with a trigonometric function, and then simplifying the resulting integral with a trigonometric identityFree Double Angle identities list double angle identities by request stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Double Angle Identities identidade tan(2x)

Cos2x Identity

1

In mathematics, an "identity" is an equation which is always true These can be "trivially" true, like " x = x " or usefully true, such as the Pythagorean Theorem's " a2 b2 = c2 " for right triangles There are loads of trigonometric identities, but the following are Prove the following identities sec 4 x – sec 2 x = tan 4 x tan 2 x trigonometric functions;X tan ⁡ 2 x = sec ⁡ 2 x I startedIn this video, we are going to derive the identity for the tangent of 2xThe identity for tan(x y) has been explained in the following videohttps//youtubTan 2x identity Tan 2x identity To evaluate this integral, let's use the trigonometric identity sin2x = 1 2 − 1 2cos(2x) Thus, ∫sin2xdx = ∫ (1 2 − 1 2cos(2x))dx = 1 2x − 1 4sin(2x) C Exercise 723 Evaluate ∫cos2xdx Hint cos 2 x = 1 2 1 2 cos ( 2 x) Answer ∫ cos 2 x d x = 1 2 x 1 4 sin ( 2 x) CCos 2x

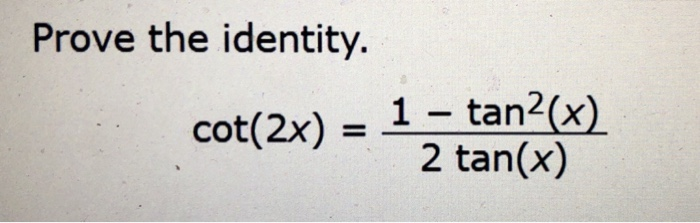
Solved Prove The Identity Cot 2x 1 Tan2 X 2 Tan X Chegg Com

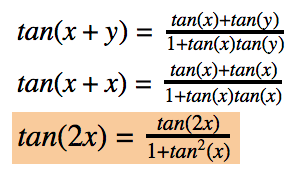
Deriving Trigonometry Identities A Visual Representation Of How Are They By Julia Fausto Maths Dover Medium

Tan^2xtan^2y=sec^2xsec^2y and, how do you factor and simplify, cscx(sin^2xcos^2xtanx)/sinxcosx MathsSs triG Consider sin(x360)sin(90x)tan(x)/cos(90x) 1ASIMPLIFY sin(x360)sin(90x)tan(x)/cos(90x) to a single trigonometric ratio Bhence or otherwise without using a calculator,solveThe half‐angle identity for tangent can be written in three different forms In the first form, the sign is determined by the quadrant in which the angle α/2 is located Example 5 Verify the identity Example 6 Verify the identity tan (α/2) = (1 − cos α)/sin α Example 7 Verify the identity tan (α − 2) = sin π/(1 cos α) Divide both side by cos^2x and we get sin^2x/cos^2x cos^2x/cos^2x = 1/cos^2x tan^2x 1 = sec^2x tan^2x = sec^2x 1 Confirming that the result is an identity

Tangent Half Angle Formula Wikipedia

Power Reducing Calculator

Integral of tan^2(x) How to integrate it step by step!👋 Follow @integralsforyou on Instagram for a daily integral 😉📸 @integralsforyou https//wwwinstagApplicants can now utilize the Public Service Portal (PSP) to apply for a Fingerprint Clearance Card (FCC)Users will be prompted to create a secure account on the PSP, allowing them to receive timely communications and to check the status of the application The new secure PSP will allow applicants the ability to fill out and submit an FCC application online and pay the associated feesSolutions to OddNumbered Exercises 1 Physical behavior should be periodic, or cyclical 3 Since cumulative rainfall is always increasing, a sinusoidal function would not be ideal here 5 y = − 3 cos ( π 6 x) − 1 \displaystyle y=3\cos \left (\frac {\pi } {6}x\right)1 y = −3 c o s(

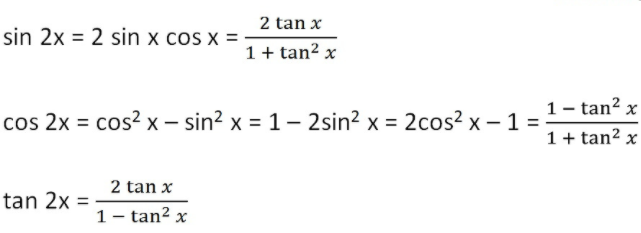
Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec

True Or False The Equation Sec 2 X 1 Tan 2 X Is An Identity Brainly Com

Verify the identitytan 2 x (1 cos 2x) = 1 cos 2x asked in Mathematics by uRanus calculus;Pythagorean identities are identities in trigonometry that are extensions of the Pythagorean theorem The fundamental identity states that for any angle θ, \theta, θ, cos ⁡ 2 θ sin ⁡ 2 θ = 1 \cos^2\theta\sin^2\theta=1 cos2 θsin2 θ = 1 Pythagorean identities are useful in simplifying trigonometric expressions, especially inTan 2 ⁡ θ = sec 2 ⁡ θ − 1 The square of tan function equals to the subtraction of one from the square of secant function is called the tan squared formula It is also called as the square of tan function identity

Ilectureonline

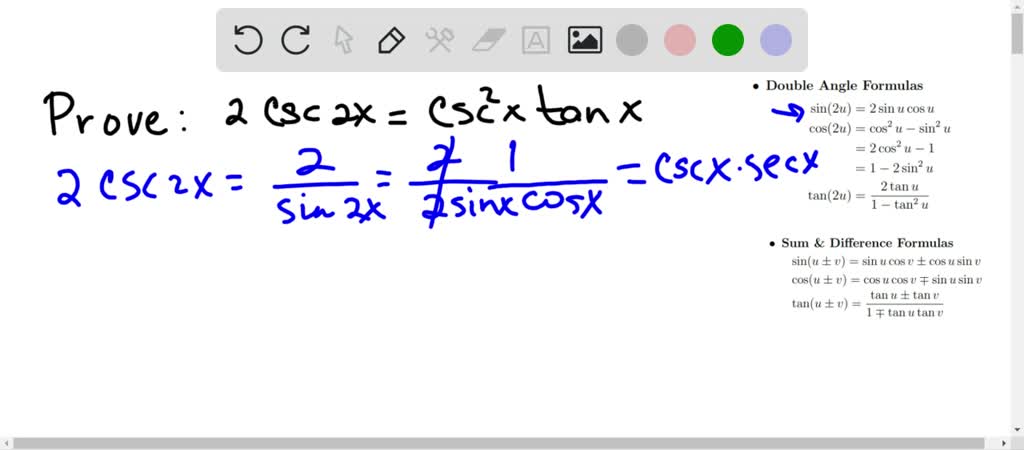
Solved In Exercises 15 22 Prove The Identity 2 Csc 2 X Csc 2 X Tan X

$$2\cot⁡4x = \cot⁡2x \tan⁡2x$$ Thank you in advance Thank you for the comments and hints I got an answer after many tries ;) Below is my answer Thank you $2cot4x = cot2x tan2x$ $2\frac{1}{tan 4x} = cot2xIdentity\\tan(2x) multipleangleidentitiescalculator identity \tan(2x) en Related Symbolab blog posts High School Math Solutions – Trigonometry Calculator, Trig Identities In a previous post, we talked about trig simplification Trig identities are very similar to this concept An identity How do you verify the equation is an identity?

Tangent Half Angle Formula Wikipedia

Integrate Tan 2x

Answer to Use a doubleangle identity to find tan(2x) \ if \ sec \ x = \sqrt {14} \ and \ sin \ x < 0 tan(2x)= By signing up, you'll getThe figure at the right shows a sector of a circle with radius 1 The sector is θ/(2 π) of the whole circle, so its area is θ/2We assume here that θ < π /2 = = = ⁡ = ⁡ The area of triangle OAD is AB/2, or sin(θ)/2The area of triangle OCD is CD/2, or tan(θ)/2 Since triangle OAD lies completely inside the sector, which in turn lies completely inside triangle OCD, we have108 Educator answers Math

What Is Tan 2x Equal To

Trig Double Identities Trigonometric Double Angle Functions Trig

 The identity, as you noted, is tan 2 x 1 = sec 2 x, for all values of x Rearranging, you absolutely get tan 2 x sec 2 x = 1 So, the original statement is false Sure, there might be values of x for which the original equation works It's solvable, but that doesn't make it true for all xFree multiple angle identities list multiple angle identities by request stepbystep This website uses cookies to ensure you get the best experience By From these formulas, we also have the following identities sin ⁡ 2 x = 1 2 (1 − cos ⁡ 2 x) cos ⁡ 2 x = 1 2 (1 cos ⁡ 2 x) sin ⁡ x cos ⁡ x = 1 2 sin ⁡ 2 x tan ⁡ 2 x = 1 − cos ⁡ 2 x 1 cos ⁡ 2 x \begin{aligned} \sin^2 x&=\frac{1}{2}(1\cos 2x)\\\\ \cos^2 x&=\frac{1}{2}(1\cos 2x)\\\\ \sin x\cos x&=\frac{1}{2}\sin 2x\\\\ \tan^2 x&=\frac{1\cos 2x}{1\cos 2x} \end{aligned} sin 2 x cos 2 x sin x cos x tan 2 x = 2 1 (1 − cos 2 x) = 2 1 (1 cos 2 x) = 2 1 sin 2

Example 5 Verify A Trigonometric Identity Verify The

2

How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic

Integrate Sec 2x Method 2

How To Use Trig Identities Mathematics Stack Exchange

Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo

Double Angle Identities Formulas Free Math Worksheets

Solve Tan 2 X 1 0 Yahoo Answers Noha Matthieu Lire Un Livre

A Trig Identity

Solve Tan2x Cot X Pi 3

Cos 2x

Tan2x Sec2x ただの悪魔の画像

Barnett Ziegler Byleen Chapter 4 Ppt Video Online Download

Solved 5 2 Verify The Following Trigonometric Identities A Chegg Com

Double Angle Identities Ck 12 Foundation

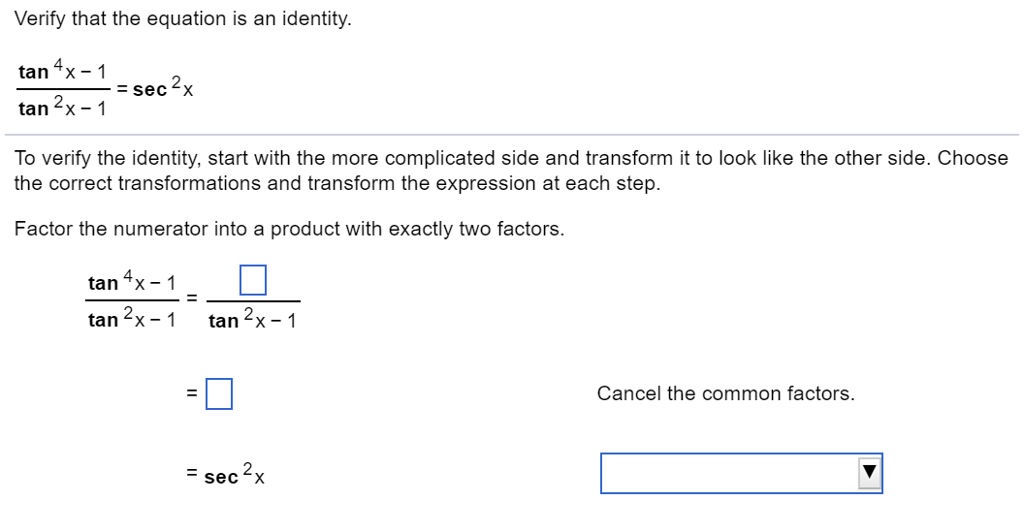
Solved Verify That The Equation Is An Identity Tan 4x 1 Chegg Com

Trig Identity Question

Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube

Art Of Problem Solving

Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube

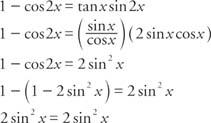
Double Angle And Half Angle Identities

Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco

Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero

Integrate Tan 2x By Parts

How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic

Prove The Identity Cos 2x 1 Sin 2x Tan P 4 X Sarthaks Econnect Largest Online Education Community

X Y X Y X Y X Y Ppt Download

8 Find An Appropriate 1 Substitution For The In Gauthmath

Q35 A Prove That Tex Frac Tan 2x Tan X Tan 2x Tan X Sin 2x Tex Snapsolve

Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities

How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Homeworklib

Cos 2x Formula Derivation Examples

What Is The Integration Of Tan 2x Solution Quora

Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help

Double Angle And Half Angle Identities Example Sin 28 Cos 2a Or Tan 2x

Trigonometry Reciprocal Identities Expii

How To Find Sin2x Cos2x And Deduce Tan2x In Terms Of Tanx Only Quora

7 Proving Ids Trig Functions Identities

Tmynyretcyocqm

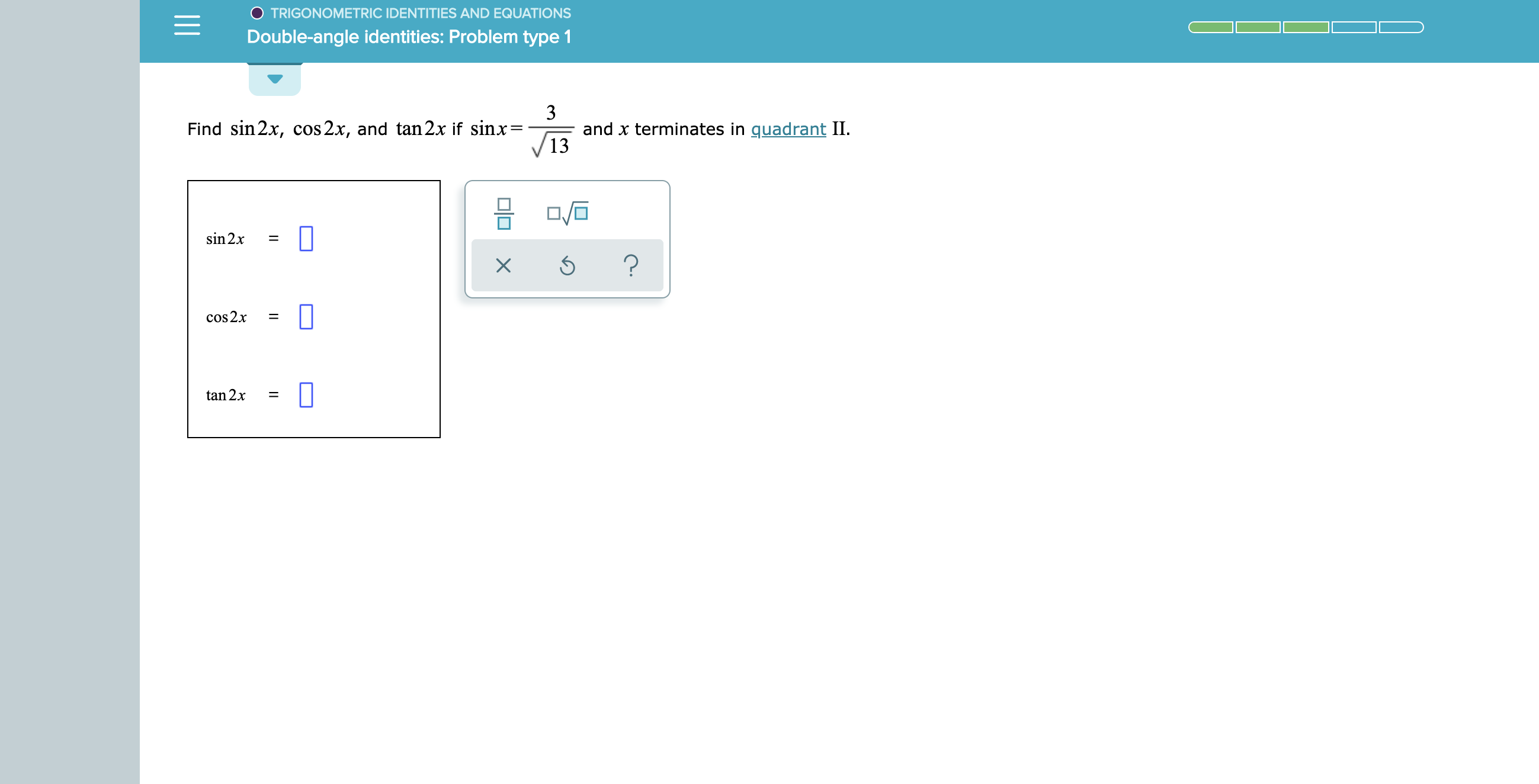
Answered Trigonometric Identities And Equations Bartleby

Solved Match Expressions In Columns A And B That Complete Chegg Com

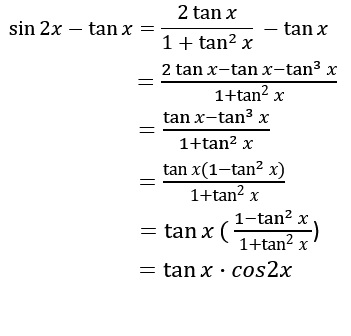
Sin2x Tanx Complete The Identity Socratic

Bestmaths Online Proof 4

View Question Trig Identities Need Help

Prove The Identity Secxcscx Tanx Cotx 2 Tan 2x Cot 2x1 Apply The Distributive Property2 Apply The Brainly Com

Tangent Half Angle Formula Wikipedia

What Is Tan 2 Theta Equal To

How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube

Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube

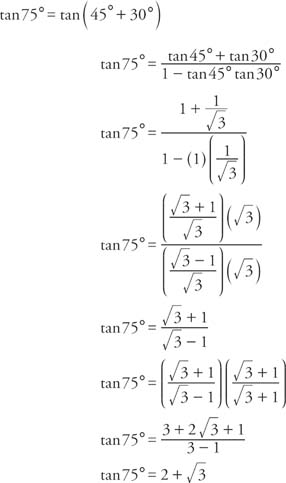
Tangent Identities

1

Solution Show All Steps Necessary To Verify The Trigonometric Identity 1 Tan 2x Csc 2x Tan 2x

How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Homeworklib

1

How To Prove Quotient And Reciprocal Identities Studypug

The Equation Sec 2x 1 Tan 2x Is An Identity True Or False

Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube

1 Point If Tan X 1 3 Cosx 0 Then Sin 2x Cos 2x Homeworklib

Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity

Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube

bestpictjcry Tan 2x Tan 2x

Solution Prove The Identity 5tan 3x 15tan X 5tan 3 X 1 3tan 2 X

How To Prove Derive Trigonometric Identities Video Lesson Transcript Study Com

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

Integrate Sec 2x Method 1

Trig Identities And Formulas Pre Calculus Quiz Quizizz

How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic

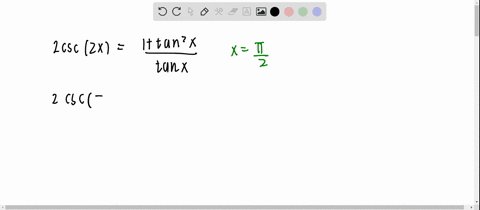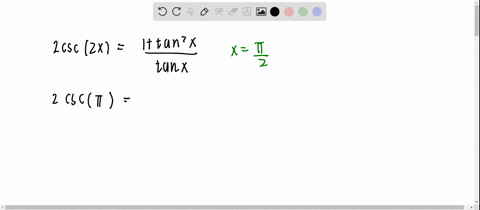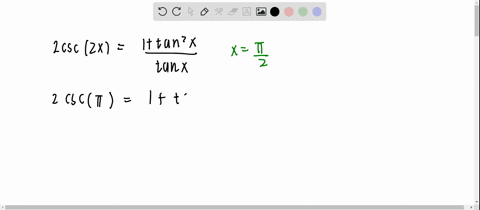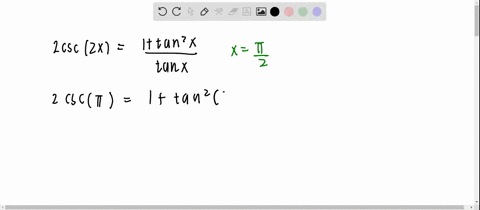
Solved Is The Identity Tan 2 X Frac 2 Tan X 1 Tan 2 X True For X Frac Pi 4 Explain

Sin 2x Formula What Is Sin 2x Formula Examples

いろいろ Tan2x 1sec2x ただの悪魔の画像

Prove The Identity Secxcscx Tanx Cotx 2 Tan 2x Cot 2x En Ya Guru

Sin 2x Cos 2x And Tan 2x

Utdallas Edu

Sum And Difference Identities Video Lessons Examples And Solutions

How Do You Prove Tan 2x Secx 1 1 Secx Socratic

What Is The Formula Of Tan2x Quora

Incoming Term: tan 2x identity, tan 2x identity proof, 1-tan^2x identity, tan^2x sec^2x identity, is sec^2x-tan^2x=1 an identity,